基础概念

函数 (Functions)

作用域到值域的一对一映射关系：

$$f:\mathbb{R}\to \mathbb{R}$$

提示

$\mathbb{R}$ 代表一维实数域。

高度图 (Height Maps)

高度图可以描述为：

$$f:{\mathbb{R}}^{\mathbb{2}}\to \mathbb{R}$$

高度图是一个 2D 图，每个像素记录了一个高度值。通常可以用高度图来描述地形 (Terrain)。

2D 参数曲线 (2D Parametric Curve)

$$f:\mathbb{R}\to {\mathbb{R}}^{\mathbb{2}}$$

也就是： $f(t)=p$ 其中 $p$ 是一个二维坐标点 (x, y)。

3D 参数曲线 (3D Parametric Curve)

$$f:\mathbb{R}\to {\mathbb{R}}^{\mathbb{3}}$$

也就是： $f(t)=p$ 其中 $p$ 是一个三维坐标点 (x, y, z)。

纹理映射 (Texture Mapping)

把纹理映射到物体表面的关系可以描述为：

$$f:\mathrm{\Omega }\to {\mathbb{R}}^{\mathbb{3}}$$

其中 $\mathrm{\Omega }$ 表示纹理域 (u, v)，${\mathbb{R}}^{\mathbb{3}}$ 表示空间域 (x, y, z)。

流形 (Manifolds)

• 1-流形：一条曲线 (Curve)
• 2-流形：一个表面 (Surface)
• 3-流形：一个体 (Volume)

弧长积分 (Arc-length Integral)

用于计算曲线的长度：

$${\int }_a^b\sqrt{(1+f^{\prime }(x{)}^2)}dx$$

连续性 (Continuity)

当函数在 $x=a$ 时，左极限和右极限存在且相等，则 $f(x)$ 在 $x=a$ 处连续，又称为 $C^0$ 连续。

$$\underset{x\to a^{-}}{lim}f(x)=f(a)=\underset{x\to a^{+}}{lim}f(x)$$

或者更正式一点：

对于给定的 $\delta >0$, 存在 $ϵ>0$，如果 $x\in (a-ϵ,a+ϵ)$，则 $f(x)\in (f(a)-ϵ,f(a)+ϵ)$。

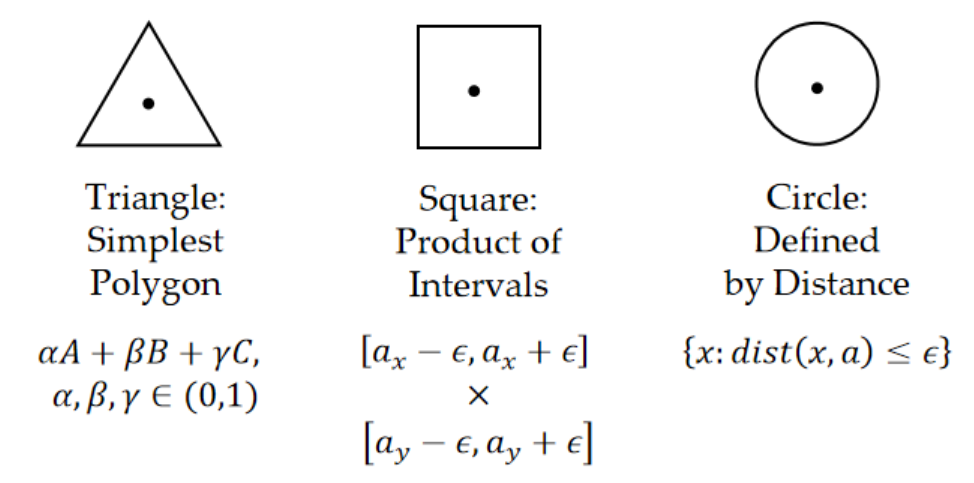
对于 2D 情况，我们使用近邻 (Neighbourhoods)。近邻可以用三角形、矩形、圆形来描述。

近邻 (Neighbourhoods)

多元函数微积分 (Calculus of Multiple Variables)

偏导数 (Partial Derivatives)

$$\frac{\partial }{\partial x}(x^{2}y+y^{3}z-xyz)=2xy-yz$$$$\frac{\partial }{\partial y}(x^{2}y+y^{3}z-xyz)=x^2+3y^{2}z-xz$$$$\frac{\partial }{\partial z}(x^{2}y+y^{3}z-xyz)=y^3-xy$$

梯度向量 (Gradient Vector)

$$\overrightarrow{\mathrm{\nabla }}f(x)=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})$$

数值微积分 (Numerical Calculus)

常用数值方法：

• 泰勒级数与展开
• 数值积分
• Lookup Table

这一部分属于 科学计算(COMP5930M) 的内容。