渲染和变换

向量点乘的应用

向量点乘的应用

向量的叉乘

$$\overrightarrow{w}=\overrightarrow{u}\times \overrightarrow{v}=\left[\begin{array}{c}{u}_y{v}_z-u_z{v}_y\\ u_z{v}_x-u_x{v}_z\\ u_x{v}_y-u_y{v}_x\end{array}\right]$$

渲染步骤

1. 描述我们的场景：每个物体的位置。
   • 变换
   • 齐次坐标
   • 四元数
2. 对我们的摄像机建模：它能看到什么？
   • 摄像机模型
3. 对感知过程进行建模：什么东西最终出现在哪里？
   • 交点/投影：不同的渲染算法
4. 对光/胶片交互进行建模：它是什么颜色？
   • 着色

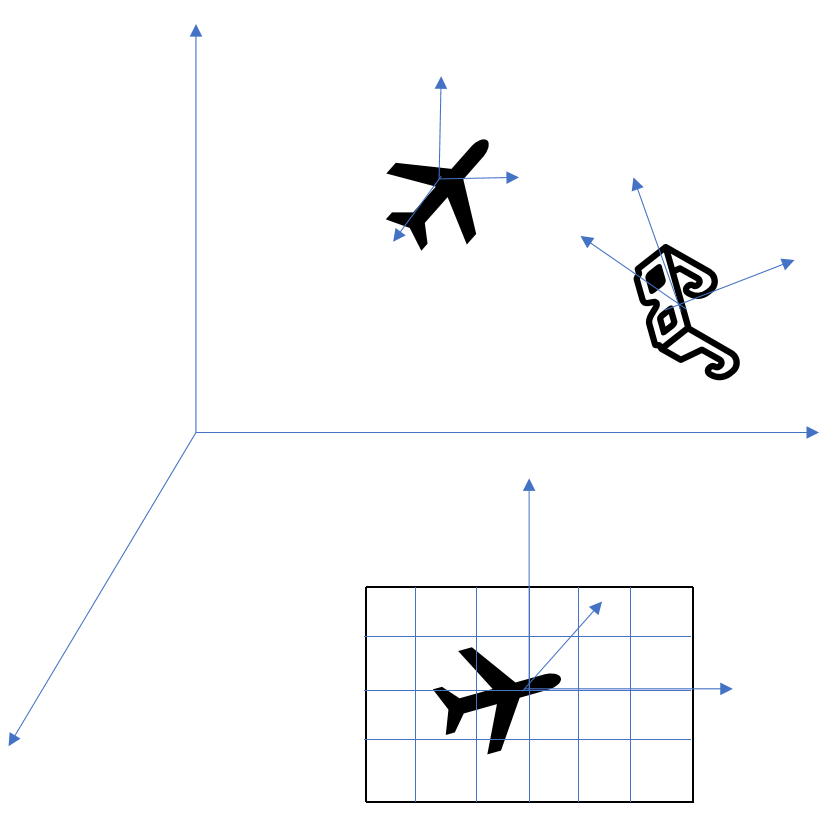
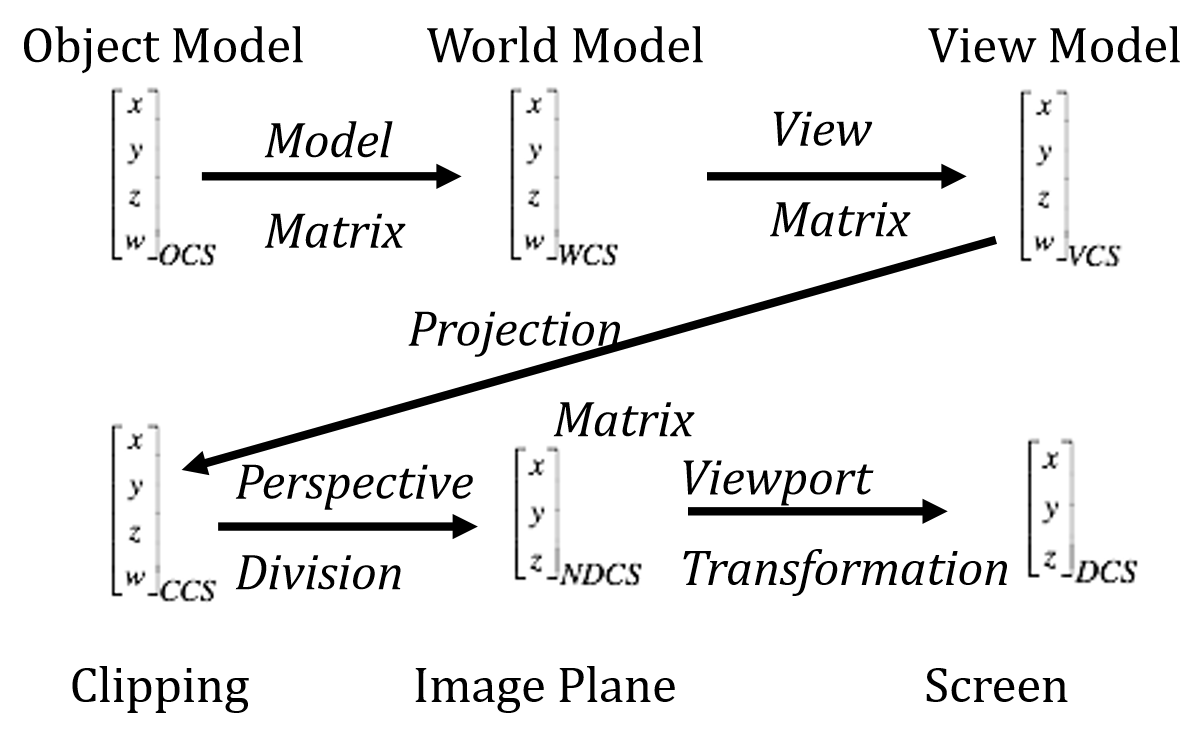
坐标系

• OCS(Object Coordinate System) 是对象坐标系。
• WCS(World Coordinate System) 是世界坐标系。
• VCS(View Coordinate System) 是视图坐标系。
• CCS(Clipping Coordinate System) 是裁剪坐标系。
• NDCS(Normalized DCS) 是标准化设备坐标系。
• DCS(Device Coordinate System) 是设备坐标系。

坐标系

通过应用矩阵来改变坐标系

为什么我们需要齐次坐标?

我们需要:

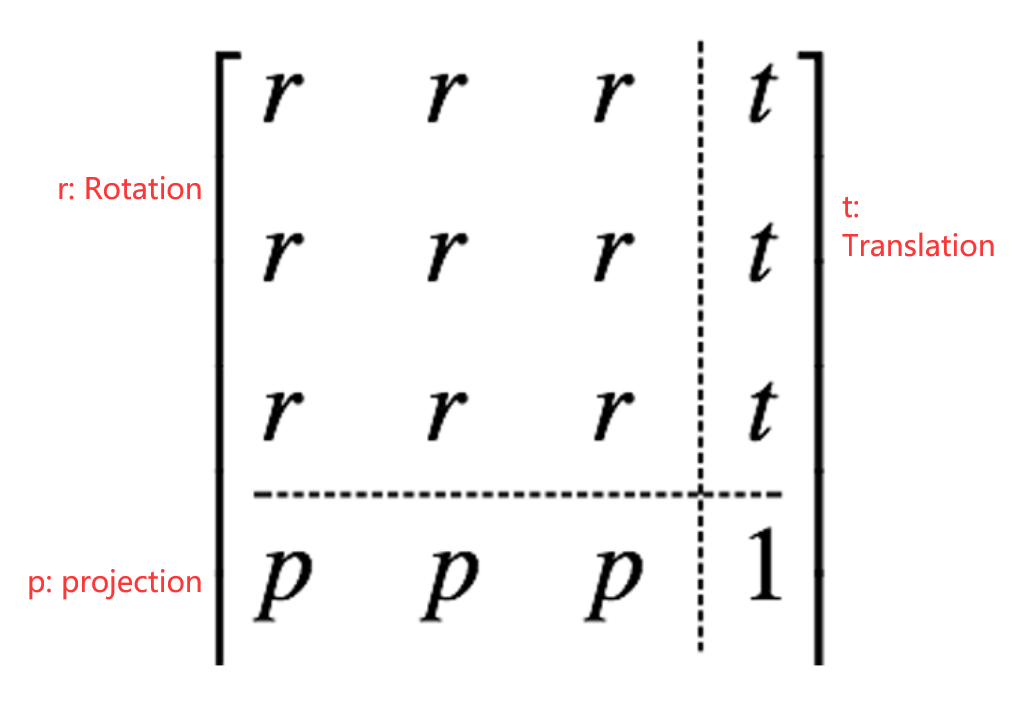
• 以矩阵形式表示平移：
  • 平移矩阵形式
• 高效地应用一系列变换：
  • 变换序列的有效应用
• 以矩阵形式表示透视：
  • 透视矩阵形式

关于变换的成本，使用齐次坐标（x, y, z, w）比使用笛卡尔坐标（x, y, z）更为高效。

齐次矩阵