Basic Concepts

Functions

A one-to-one mapping from the domain to the range:

$$f: \mathbb{R} \to \mathbb{R}$$

Note

$\mathbb{R}$ represents the one-dimensional real number domain.

Height Maps

A height map can be described as:

$$f: \mathbb{R^2} \to \mathbb{R}$$

A height map is a 2D image where each pixel records a height value. It is commonly used to represent terrain.

2D Parametric Curve

$$f: \mathbb{R} \to \mathbb{R^2}$$

In other words: $f(t) = p$ where $p$ is a two-dimensional coordinate point (x, y).

3D Parametric Curve

$$f: \mathbb{R} \to \mathbb{R^3}$$

In other words: $f(t) = p$ where $p$ is a three-dimensional coordinate point (x, y, z).

Texture Mapping

The relationship mapping a texture to an object's surface can be described as:

$$f: \Omega \to \mathbb{R^3}$$

Here, $\Omega$ represents the texture domain (u, v), and $\mathbb{R^3}$ represents the spatial domain (x, y, z).

Manifolds

• 1-Manifold: A Curve
• 2-Manifold: A Surface
• 3-Manifold: A Volume

Arc-length Integral

Used to calculate the length of a curve:

$$\int_{a}^{b} \sqrt{(1+f'(x)^2)} dx$$

Continuity

When the left limit and right limit exist and are equal at $x = a$, then $f(x)$ is continuous at $x = a$, also known as $C^0$ continuity.

$$\lim_{x \to a^-} f(x) = f(a) = \lim_{x \to a^+} f(x)$$

Or more formally:

For a given $\delta > 0$, there exists $\epsilon > 0$ such that if $x \in (a - \epsilon, a + \epsilon)$, then $f(x) \in (f(a) - \epsilon, f(a) + \epsilon)$.

For the 2D case, we use neighborhoods. Neighborhoods can be described using triangles, rectangles, or circles.

Neighborhoods

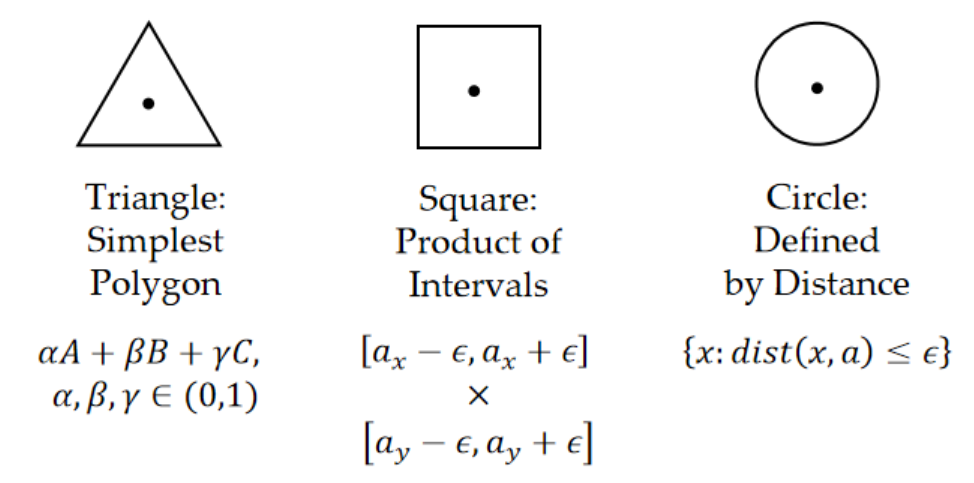
Calculus of Multiple Variables

Partial Derivatives

$$\frac{\partial}{\partial{x}}(x^2y + y^3z - xyz) = 2xy - yz$$

$$\frac{\partial}{\partial{y}}(x^2y + y^3z - xyz) = x^2 + 3y^2z - xz$$

$$\frac{\partial}{\partial{z}}(x^2y + y^3z - xyz) = y^3 - xy$$

Gradient Vector

$$\vec{\nabla} f(x) = (\frac{\partial{f}}{\partial{x}}, \frac{\partial{f}}{\partial{y}}, \frac{\partial{f}}{\partial{z}})$$

Numerical Calculus

Common numerical methods:

• Taylor Series and Expansion
• Numerical Integration
• Lookup Table

This section belongs to the content of Scientific Computation (COMP5930M).